The Monty Hall Paradox: A probabilistic approach to judgement errors
- Atharv Raturi
- Nov 23, 2022
- 7 min read

ABSTRACT
This review article tackles the infamous Monty Hall Paradox, or the Monty Hall Problem, with the aim of developing and inducing an intuition for this counter intuitive “riddle” of mathematics. To model the problem, we shall investigate the concepts of Classical conditional probability and take a dive into Bayes’ approach as well. The Monty Hall problem also finds various applications in data science and quantum computing, thus strengthening the scope of this concept.
KEYWORDS
Conditional Probability, Bayesian probability, Proposition, MHP, Frequentist, Hot hand, Principle of Restricted Choice, Bayesian updating, Game Theory, Neumann’s Minimax theorem, Minimax strategy
INTRODUCTION
It is not very often that our logic and instincts are at a clash, influencing our decision-making immensely in cases that may be relatively minor or downright life changing. Most people, having been told to trust their guts, tend to follow their instincts in such situations without giving it much thought, clearly defining themselves in the win mentally. Are they in for a rude awakening? Does logic have the upper hand in this decisive battle?
Imagine a scenario where you are an owner of a bookshop with two regular customers, Ralph and Zeke. Whereas Ralph is open to all genres of reading, Zeke is particularly interested in horror readings. An order is placed- that of a horror novel. Who do you think placed the order?
While intuitively it might seem that both customers are equally likely to order the horror book since Ralph is indifferent to the choice and Zeke is not, the reality is that the novel was likely ordered by Zeke. The reason is that our intuition doesn’t consider the fact how the two customers are choosing the books. While the answer to the problem above may become easily intuitive, difficulty arises when larger sample sizes are taken into consideration such as in the famous Deal or No Deal game. Hence, probabilistic attempts are made to account for this fallacy, known as the Monty Hall Paradox.
2.0 The Monty Hall Problem (MHP)
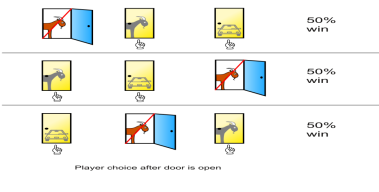
The host of a game show asks a contestant X to choose one of the three closed doors in front of him. Only one door has a prize (a car) on the other side while the other doors have a goat behind them. Once X makes the first choice, the host will reveal the contents behind another door, and then finally ask the contestant to either stick with his previous door choice or switch to the remaining door. What should the contestant X do to maximize his probability of winning the car?
A common approach to this problem would be finding the probability of the car being in the first choice which is 1 in 3 and concluding that since only two doors remain and one has a car while the other does not, the probability of winning would be 1 in 2 irrespective of the door choice. However, is this approach which seems completely logical correct?
Well, not only is this approach incorrect but also choosing one of the options over the other downright doubles the probability of winning!
2.1 Stay or Switch?
Multiple intuitive arguments can be made on why one should switch, but when we use the concepts of Bayesian probability (which is largely based on Conditional probability), things tend to favour counter-intuition more. For instance, finding the car in the first turn has a 1 in 3 chance. If it does happen, then staying is good because the other two doors have goats. Complementarily to this, the first chosen door having the goat is a 2 in 3 probability. Then, staying is not good. However, switching surely gives the car, as the host must reveal the goat behind another door, while the remaining one then has the car behind it.[1]
Hence, more often than not, switching will win you a prize with a probability of 2 in 3 which is double of the probability of winning when staying i.e., 1 in 3.
2.2 Lapse in Judgement
Understanding the concept of this problem might be a bit difficult for a common person but a frequentist would easily grasp the principle. Interestingly enough, although people find switching or staying equally likely, most of them would rather stay than switch. The numbers are as high as 80-90% (Friedman 1998). Thus, people feel compelled to stay with their first choice by an overwhelming propensity.[2]
While judging the probabilities as equal, they also feel extremely confident with their choice (cf. Falk, 1992). Hence, it is not difficult to realize that people stick with their intuitions to various degrees.[2]
2.3 MHP not as a Riddle
Looking at the problem mathematically, we understand that quite a few assumptions are made; the more we assume, the more we conclude, but more limited are our conclusions. There might not be one mathematical solution as a true answer but a range of solutions. Also, the meaning of the conclusions is affected by the way we make probabilistic assumptions. That being said, sometimes what we fail to see is that the contestant has to think about the first choice as well. For this action, we should consider that the contestant has two decisions to make in the game rather than one.[3]
3.0 Principle of Restricted Choice
Among various intuitive conclusions, people also tend to believe that “success breeds success”. For instance, if an athlete is performing great, they will continue to do so. This concept is called the hot hand phenomenon. It is widely cited by sportspersons, but like many widely accepted assumptions probability has proven that it is completely unfounded. While it leads us to the principle on which all of MHP is based, hot hand is a “massive and widespread cognitive illusion” (Kahneman, 2011).[4]
3.1 The Principle
If we now reconsider the Bookshop situation earlier discussed, we shall arrive on the conclusion that Zeke is more restricted to choose the horror novel. While Ralph may order that book, Zeke must. Hence, on finding out the order has been placed, our guess of who ordered the book should tilt towards Zeke. This is the principle of restricted choice. It supplies a way by means of an informal intuition to shift in a certain direction on the intake of newly acquired information. It encapsulates the qualitative feature of Bayesian updating. It stipulates that if the arriving information is true, the odds in favour of a proposition increase, or conversely, if the information is false, the odds in favour of a proposition decrease.[5]
3.2 Problems similar to MHP based on the Principle of Restricted Choice
Bertrand’s Box Paradox
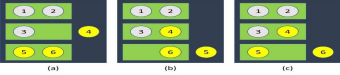
There are 3 visually identical caskets, where one has two gold coins, another has two silver coins, and the remaining contains a gold and a silver coin. Let us suppose that we draw a coin from any of the caskets and it turns out to be gold. What is the probability the other coin is gold as well?
Since a gold coin is drawn, the silver coin casket is out of the equation; only the gold and the mixed casket remain. While it may be intuitively appealing to assign equal odds to the remaining gold coin being from either of the two caskets, an important nuance is ignored. The initial draw from the gold casket is more restricted to choose the gold coin whereas a draw from the mixed casket may or may not give a gold coin. This makes one of the odds twice as restricted as the other. Thus, by the principle, the updated probabilities of the initial draw being from the gold casket is 2:1, double that of 1:1 (the prior probabilities), which in turn implies that the odds of other coin being gold is 2 in 3 rather than 1 in 2.[6]
Boy or Girl Paradox
Mr. Wayne is a father of two. While walking down the street he proudly introduces the young boy at his side to be his son. What is the probability that his other kid is also a boy?
The intuitive answer is ½, which is correct. However, the reason that brings us to this conclusion is usually false. If we assume that Mr. Wayne randomly chose on of his children for a walk, the problem becomes similar to the Bertrand’s Box Paradox. The difference is that the mixed gender group of solutions has greater prior odds (1:2) than any single gender group. On learning that a boy is walking with Mr. Wayne, the posterior odds in favour of two boys as his son become double the prior odds i.e., 1:1. Due to this the odds that Mr. Wayne has two sons is 1:2. Hence, the probability of the other child being a boy is 1:2 as well.[7]
4.0 Conclusion: Future scope of MHP
The intriguing concepts of the Monty Hall Paradox have proven their resourcefulness in Data science repeatedly. From analysing business proceedings to predicting financial models, it has provided a deeper insight into data which cannot be easily ignored. Data scientists have started incorporating MHP along with the Principle of Restricted Choice into Quantum computing,
positively looking forward to the day when the erratic behaviour of quantum units such as quarks can be strongly predicted under certain conditions.
As how it initially flourished, MHP will forever have a huge presence in the field of Games, tricks and cons. Its forms a foundation for Game Theory- if in the MHP game both the contestant and the host will try to beat the other. This is Neumann’s minimax theorem where the game has a value p. If the contestant uses his minimax strategy, he will win regardless of the strategy of the host, while if the host uses his minimax strategy, the contestant will win with a probability at max p. Game theory has been modified multiple times to assist in the fields of Molecular Physics, Actuarial Science, Computer Science etc.
Enhancing ourselves with these aspects of probability will help industries make better forecasts and provide better evidence on cases. With better knowledge, such concepts can be used in predicting disease rises, epidemic blowouts, and make ourselves better equipped to deal with arising “counter-intuitive” situations.
References -:
[1] The Monty Hall Problem, Richard D. Gill, Mathematical Institute, University of Leiden, Netherlands (17th March,2011).
[2] Thinking and Reasoning, 2003, 9(1), 67-90, Ana M. Franco-Watkins, University of Maryland, College Park, USA,
Peter L. Derks, The College of William & Mary, Williamsburg, VA, USA, Michael R.P. Dougherty, University of Maryland, College Park, USA.
[3] Statistica Neerlandica (2011) Vol. 65, nr. 1, pp. 58-71, “The Monty Hall Problem is Not a Probability Puzzle.” Richar D. Gill, Mathematical Institute, University of Leiden, Netherlands.
[4] Bar-Hillel, Maya, and Ruma Falk. 1982. “Some Teasers concerning Conditional Probability.” Cognition 11(2): 109-22.
[5] Joshua B. Miller and Adam Sanjurjo. “A Bridge from Monty Hall to the Hot Hand: The Principle of Restricted Choice”. Journal of Economic Perspectives Volume 33, Number 3- Summer 2019- Pages 144-162.
[6] Bertrand 1889; Gorrochurn 2012; presentation below adapted from Rosenhouse 2009)
[7] Gigerenzer, Gerd, and Ulrich Hoffrage. 1995. “How to improve Bayesian Reasoning without Instruction: Frequency Formats.” Psychological Review 102(4): 684-704.



Comments